MIC

Overview
Project contributions
Areas of improvement

Overview

This is a project that I started work on when I was working at OFCE, and was having discussions with colleagues heavily involved in developing Agent-Based Models (ABMs), esentially bottom-up simulations of an economy which allow for great flexibility in the rules that agents are endowed with, and in turn often generate very interesting emergent phenomena.

While the computational nerd in me was interested in these models for their own sake, the researcher was more intrigued by the problem of validating these models empirically. Here, the lovely modeling flexibility of being able to specify all manner of behavioural rules creates a problem: the models are generally not invertible, do not possess well-defined likelihood functions, and generally can only be simulated. A big challenge facing this research agenda (which persists to this day) is how to:

Estimate the deep behavioural parameters of these models from empirical datasets.
Compare the relative performance of different models of the same phenomenon, in other words how to perform model selection.

By that time (around 2008) there were already plenty of estimation methods for pure simulation models, most based on some form of indirect inference or simulated method of moments. Scaling the methods to larger ABMs was a challenge (which I try to tackle with my BEGRS project), but this prompted me to focus on the second problem.

The result of this effort was the Markov Information Criterion (MIC), initially outlined in (Barde, 2017), which extends the concept of the Akaike Information Criterion (AIC) (Akaike, 1974) to Ntth order Markov processes. The idea, like the AIC is to provide an unbiased estimate of the cross-entropy of a model relative to an empirical dataset, however, the MIC only requires that models be able to generate simulation data, and the cross entropy measurement is made between the simulated and empirical data. In this manner, any model able to generate simualtions can be compared.

Formally the cross entropy estimate is obtained by using the length of the compressed data generated by a compression algorithm trained on the simulation data, in line with the concept of minimum description length, described by (Grünwald, 2007). Because Jensen’s inequality implies that any measurement of cross entropy is biased, the key to obtaining an unbiased measurement was to choose a compression algorithm with known and predictable bias, in order to be able to perform a bias correction (Note, this is similar to the role of the ‘penalisation term’ in the AIC, which is in fact there to correct the bias of using the maximised value of the likelihood as the estimate of cross entropy).

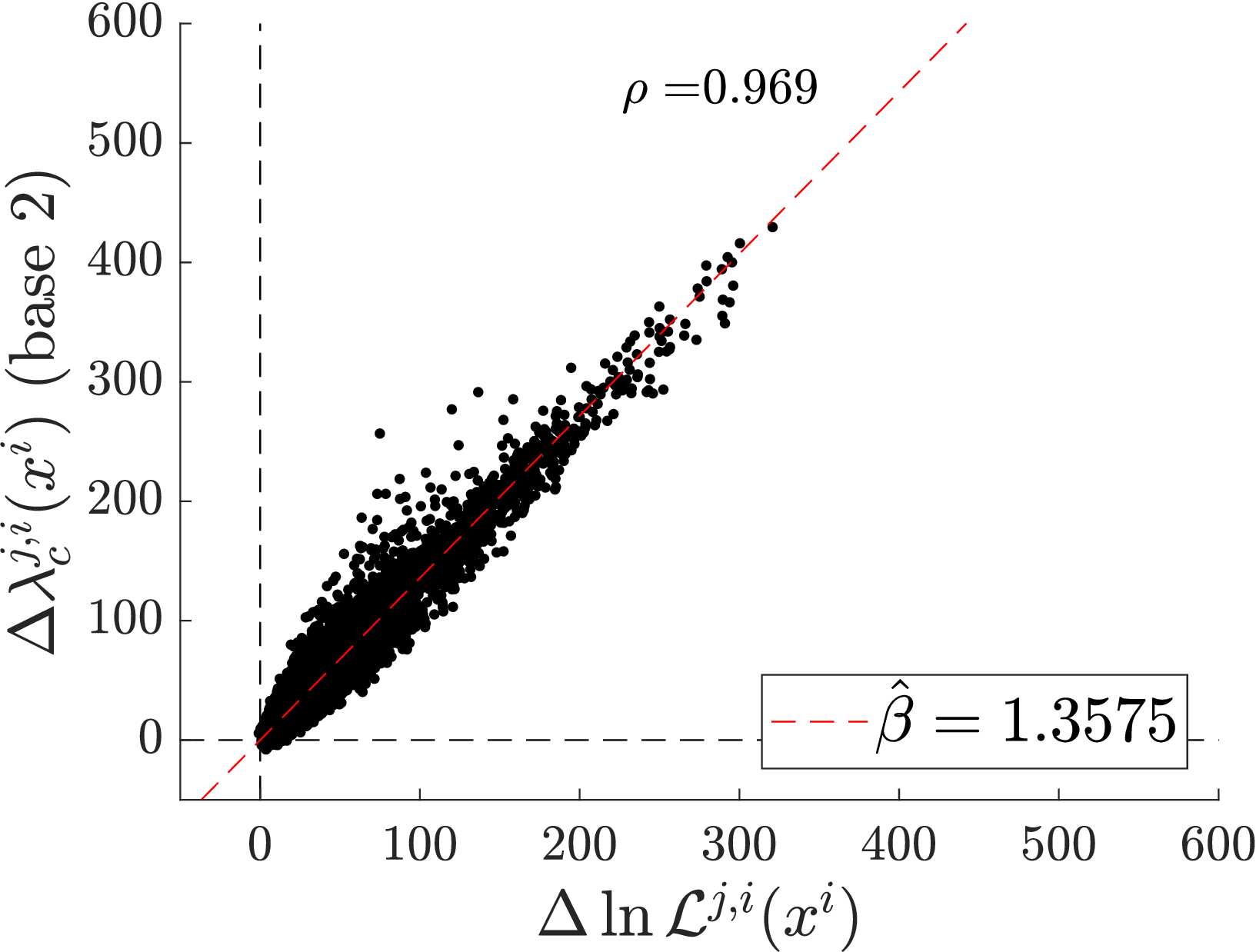
The algorithm used as the basis of the MIC is the Context Tree Weighting (CTW) compression of (Willems et al., 1995), which is proven to achieve the Rissanen bound, which is the maximum achievable compression efficiency. The details of this are provided in the paper (Barde, 2017), however the key feature that enables the CTW compression method to achieve the theoretical Rissanen bound is the fact that it relies on the Krichevsky-Trofimov (KT) estimator (Krichevsky & Trofimov, 1981) to provide the estimate the probability that a given bit of data will be 1, conditional on the information in the context. Because the CTW, using KT estimators at the bit-level, achieves the Rissanen bound, and the formula for the bound is know, it is possible to subtract this theoretical bound from the description length and obtain an unbiased measurement of the cross entropy between the model (as embodied in the training data that it has generated) and the empirical data.

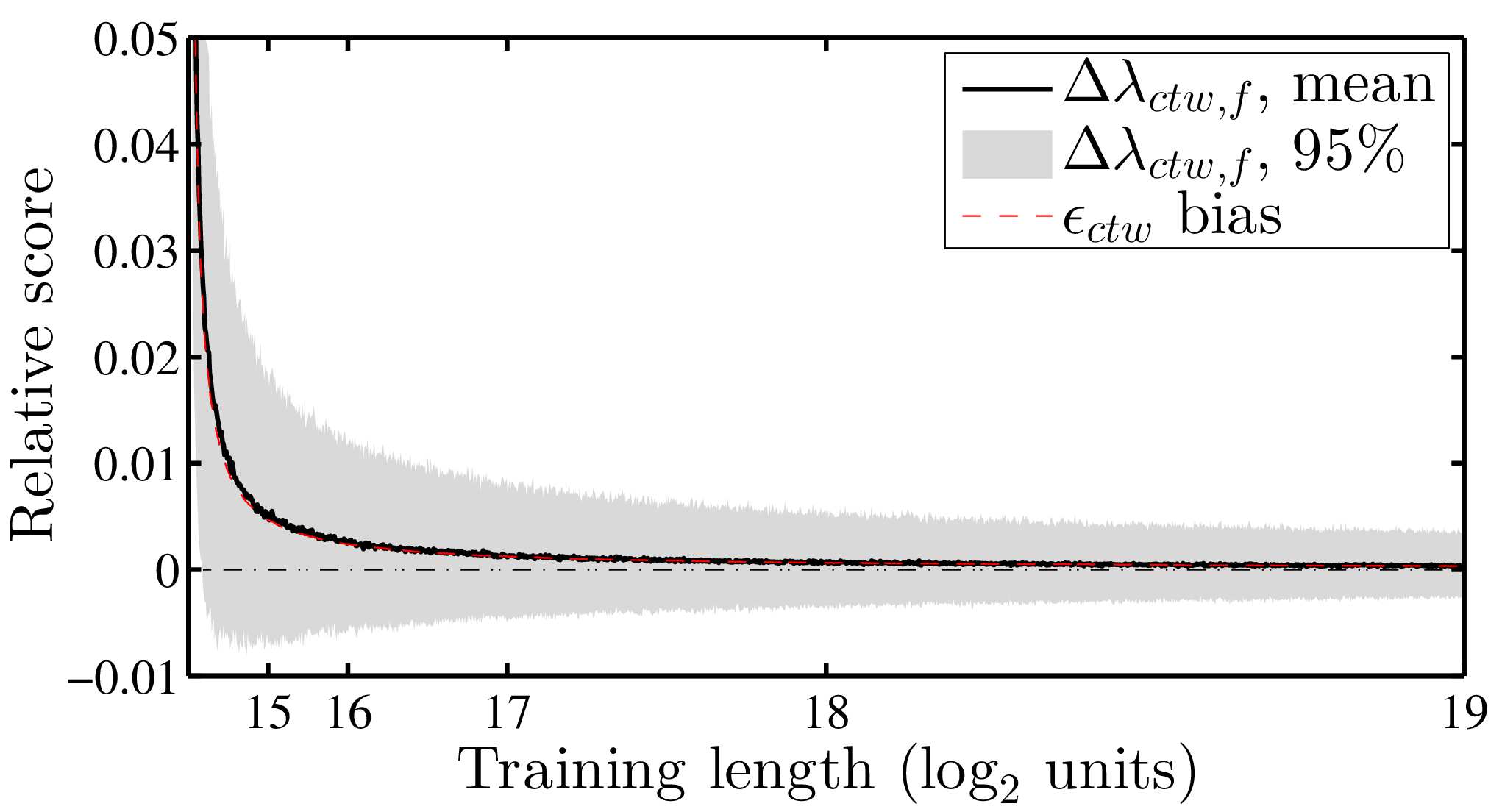
Description length of an i.i.d beta variable given training length

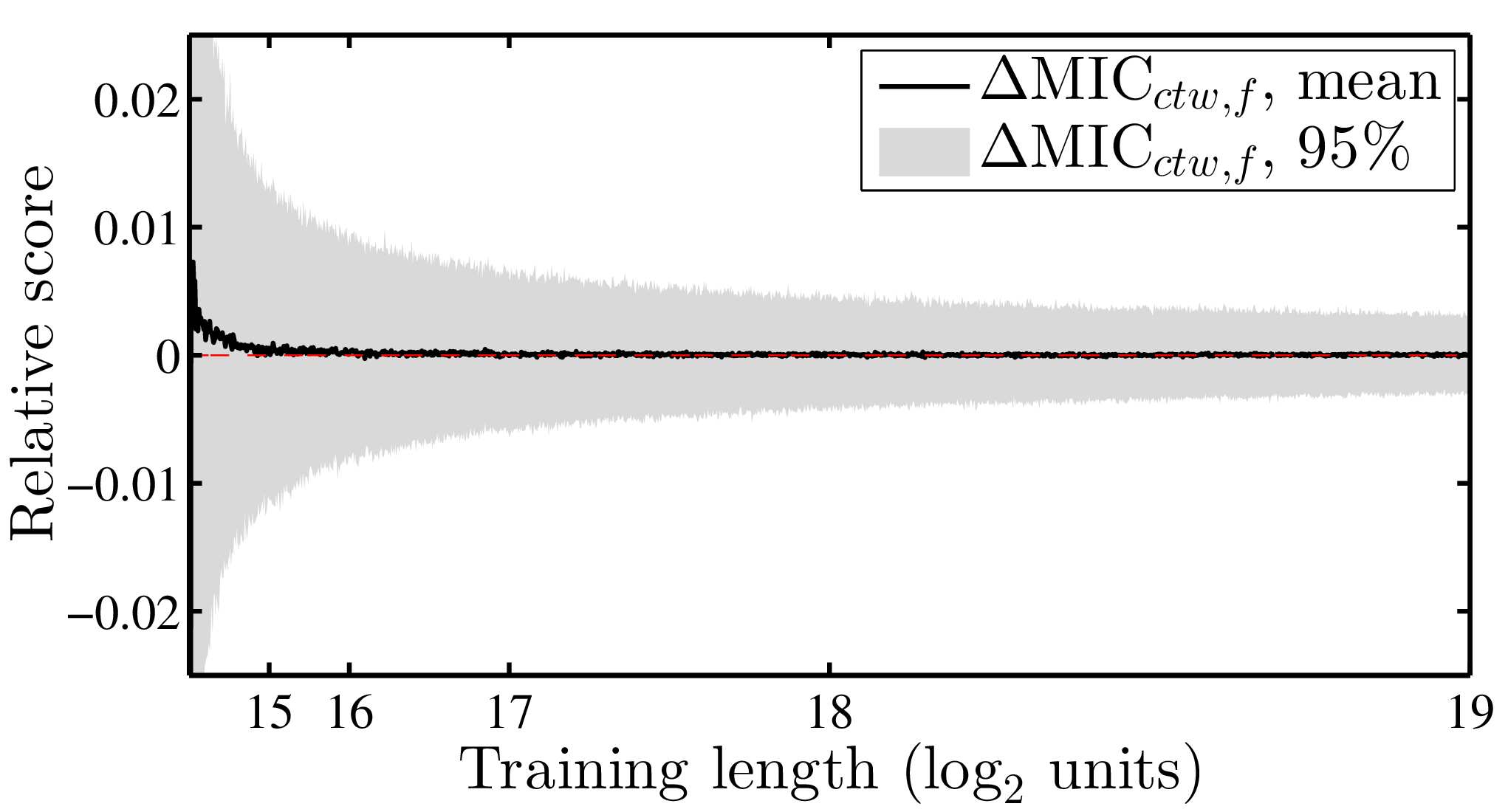
MIC of an i.i.d beta variable given training length

The CTW algorithm provides near-optimal compression, achieving the Rissanen bound. On the left plot, the mean description length for Monte Carlo replications of some testing data is plotted against the amount of training data, with the theoretical bound overlaid. Because the expected description length matches the theoretical bound, the plot on the right shows that when subtracting the bound from the description length to obtain the MIC, one obtains an unbiased, if noisy, measurement of the cross entropy.

In principle, this allows for comparison of any model that (a) can generate simulated data and (b) is reducible to an Nth order Markov process. The plots below show the output of two tests, on which compares a range of univariate ARMA-ARCH specifications, the other which compares a range of multivariate (Smets & Wouters, 2007) models. In both cases, the MIC scores are compared to the existing goodness-of-fit measure and show relatively good agreement.

Scatter plot of MIC score vs. log-likelihood for ARMA-ARCH models

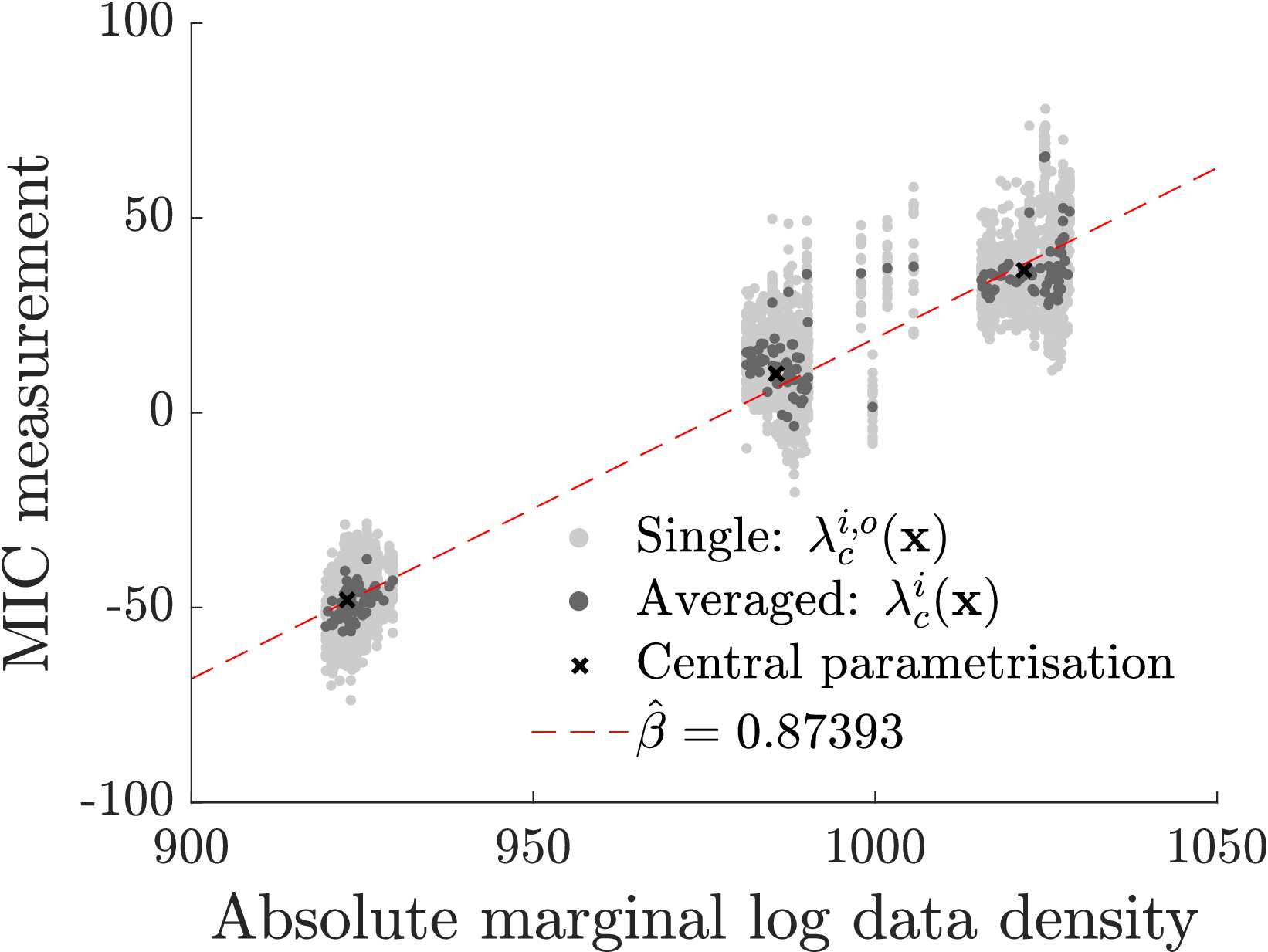
Scatter plot of MIC score vs. posterior density for DSGE models

The MIC maps (noisily) to standard goodness-of-fit measures. On the left plot, MIC scores are plotted against the log-likelihood for an ARMA-ARCH process on the right, MIC scores are plotted against the posterior density for 3 different versions of the Smets Wouters model.

While the MIC provides an unbiased measurement of cross entropy, this measurement is noisy, as visible in both sets of plots above. I suppose this is not surprising in itself given that the method relies both on simulated and empirical data, both of which will suffer from sampling error. A nice feature, in this respect, is that the method scores each observation separately, with the overall MIC being the sum of the scores over observations. This allows for two interesting extensions:

First, if a long enough time-series is available, the relative goodness of fit can be assessed over time, and not just on the aggregate data.
Second, because scores are available for each observations, the Model Confidence Set methodology of (Hansen et al., 2011) can be applied to scores obtained for a set of models on the same data, statistically establishing which subset of models offers superior performance.

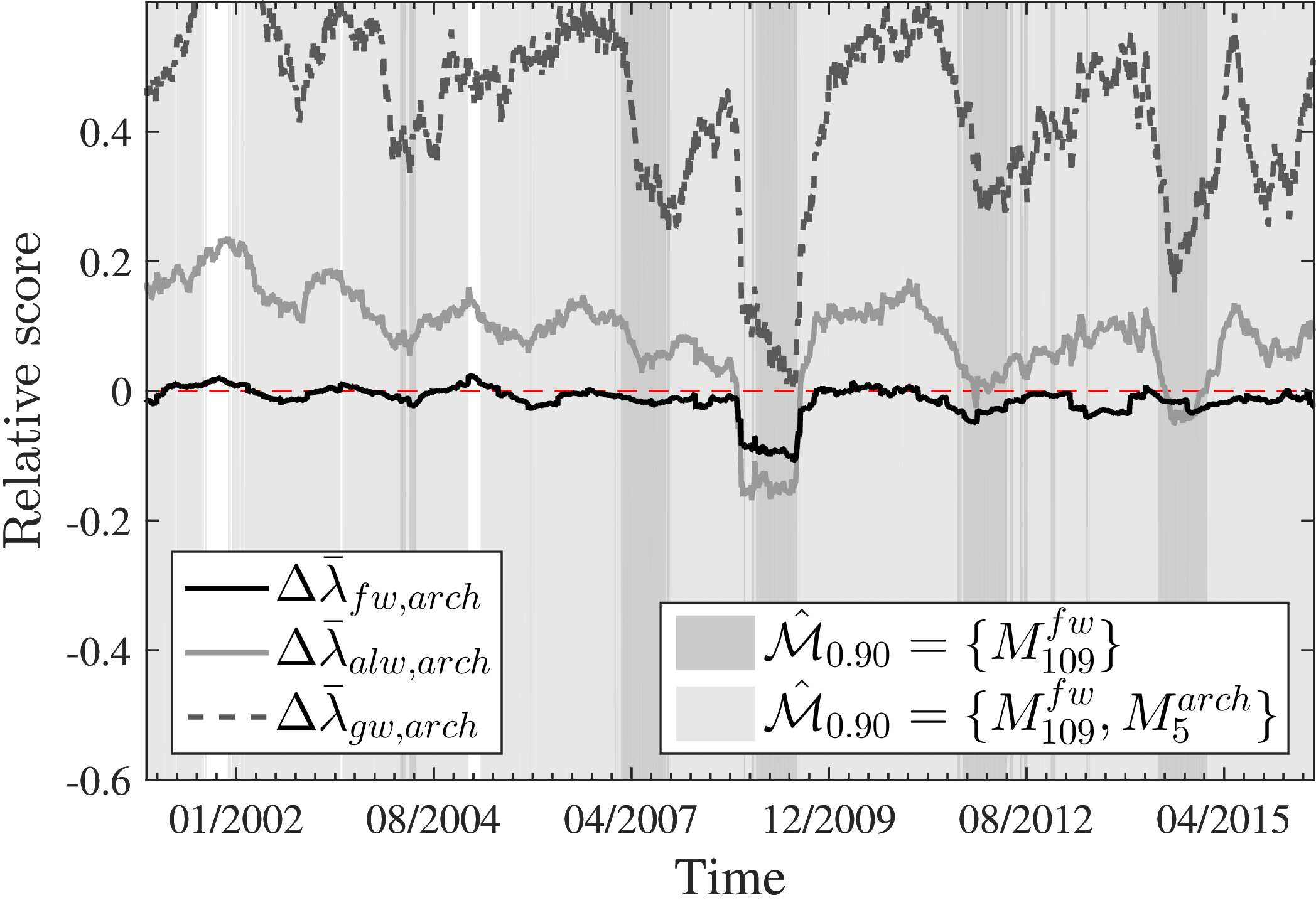
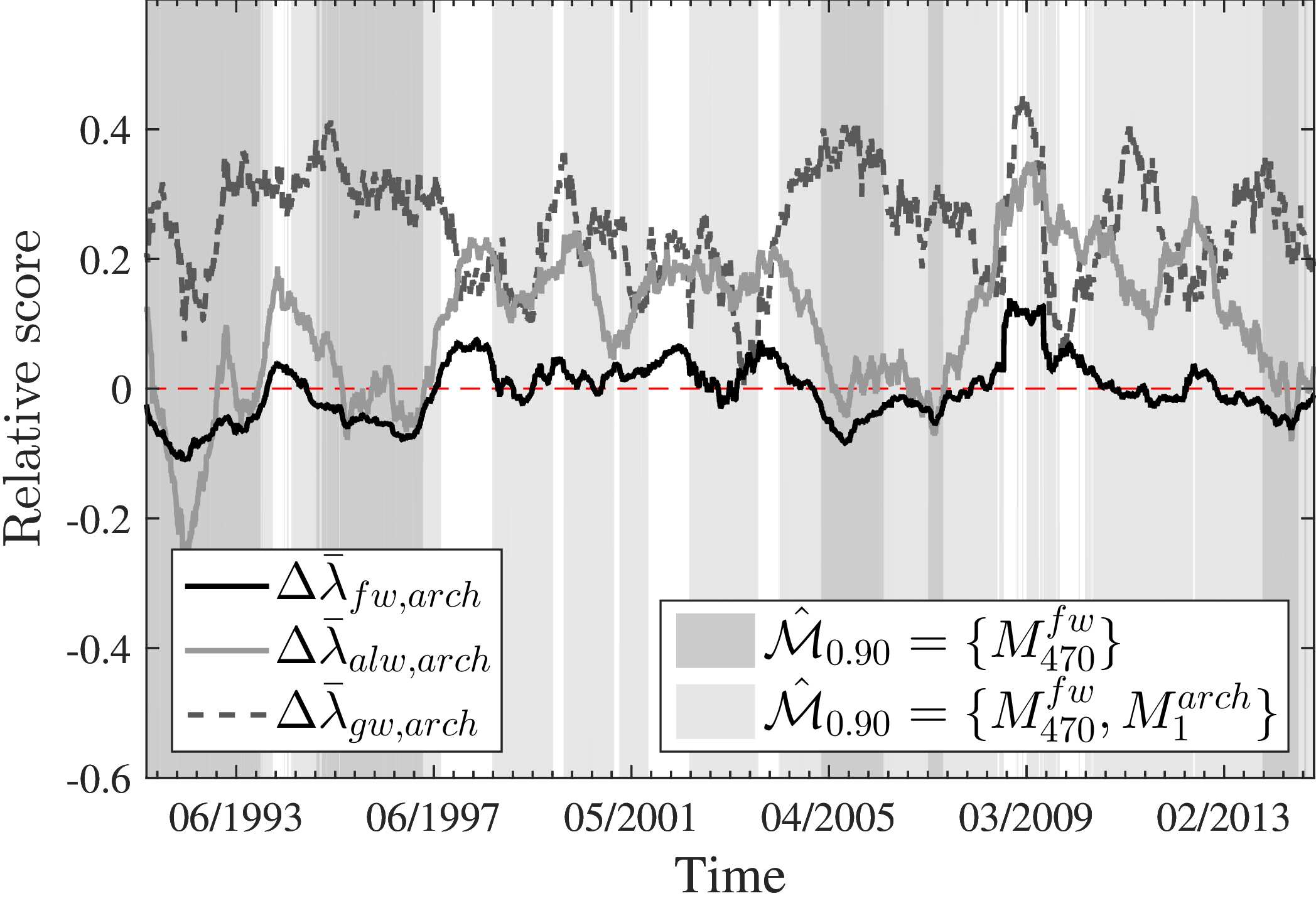
A good illustration of this is provided in (Barde, 2016), which applies the MIC to ABMs of herding in financial markets. Here the ABMS of (missing reference), (Alfarano et al., 2005) and (Franke & Westerhoff, 2011), which are all based on the recruitment mechanism of (Kirman, 1993), are tested against a set of benchmark ARCH-GARCH specifications. The result of this work was to establish a clear ranking in performance between ABMs on the data, with the best-performing ABM providing equivalent performance to the best ARCH-GARCH specification. Interestingly, and visible in the plots below, the performance of all 3 ABMs is markedly improved during the financial crisis, which provides some support to the claims that ABMs are better able to account for periods of turmoil.

Relative MIC scores of 4 model classes on the USD-YEN exchange rate

Relative MIC scores of 4 model classes on the DAX index

Thiese examples, taken from the 2016 direct comparison paper, show how the MIC tracks the relative performance of 3 ABMs against an ARCH-like benchmark for stock indices (left) and exchange rates (right). Note the improvement in relative scores for all ABMs during the 2008 financial crisis!

Project contributions

What bits does this project reach that others don’t?

For me, the most important aspect is to provide a reliable benchmark for validation of ABMs, essentially providing a proof-of-principle that it is entirely possible to compare these kinds of models to existing benchmarks. On a personal note, I tend to think that the validation problem limits the adoption of such models, and having tools that can do this is important.
A nice aspect is the fact that the noisiness of the measurement, which I guess was always going the be there, can be counteracted by techniques such as the MCS.

Areas of improvement

Things I’m not that happy about right now.

A first limit is the fact that the multivariate version of the MIC (Barde, 2020), while functional, requires a lot more computational overhead compared to the univariate version. While it is feasible to use it on multivariate models, it very quickly reaches its limit.
The code provided in the Github repo uses Cython to improve the computation speeds. This is clunky, to be honest, as it requires potential users to compile the C code on their platform, which is a pain. It is probably the case that the whole thing needs refactoring using a more modern and efficient implementation. Something for my to-do list?
Finally, the noisiness of the measurement (not to mention the computational cost of calculation) means that the MIC should not be used as an objective function as part of estimation of simulation models. It is a ‘post-estimation’ method only! I had a hope, initially, that this might be possible, but it turns out not to be practical. More on that in the BEGRS project…

The paper aims to address the issue of comparing agent-based models (ABMs) with more traditional VAR and DSGE models by developing a multivariate extension of the Markov Information Criterion (MIC) of Barde (2017). The univariate MIC measures the informational distance between a simulation model and some empirical data by mapping the simulated data to a Markov transition matrix, and is proven to provide an unbiased measurement for all models reducible to a Markov process. As a result, the MIC can accurately measure distance using only simulated data, for a wide class of data generating processes. The paper first presents the multivariate extension of the MIC and its validation on VAR and DGSE models before carrying the first direct comparison between a macroeconomic ABM and a DGSE model, namely the benchmark ABM of Caiani et al. (2016) and Smets and Wouters (2007).

The recent increase in the breath of computational methodologies has been matched with a corresponding increase in the difficulty of comparing the relative explanatory power of models from different methodological lineages. In order to help address this problem a Markovian information criterion (MIC) is developed that is analogous to the Akaike information criterion (AIC) in its theoretical derivation and yet can be applied to any model able to generate simulated or predicted data, regardless of its methodology. Both the AIC and proposed MIC rely on the Kullback–Leibler (KL) distance between model predictions and real data as a measure of prediction accuracy. Instead of using the maximum likelihood approach like the AIC, the proposed MIC relies instead on the literal interpretation of the KL distance as the inefficiency of compressing real data using modelled probabilities, and therefore uses the output of a universal compression algorithm to obtain an estimate of the KL distance. Several Monte Carlo tests are carried out in order to (a) confirm the performance of the algorithm and (b) evaluate the ability of the MIC to identify the true data-generating process from a set of alternative models.

The present paper tests a new model comparison methodology by comparing multiple calibrations of three agent-based models of financial markets on the daily returns of 24 stock market indices and exchange rate series. The models chosen for this empirical application are the herding model of Gilli and Winker (2003), its asymmetric version by Alfarano et al. (2005) and the more recent model by Franke and Westerhoff (2011), which all share a common lineage to the herding model introduced by Kirman (1993). In addition, standard ARCH processes are included for each financial series to provide a benchmark for the explanatory power of the models. The methodology provides a consistent and statistically significant ranking of the three models. More importantly, it also reveals that the best performing model, Franke and Westerhoff, is generally not distinguishable from an ARCH-type process, suggesting their explanatory power on the data is similar.

Table of contents

Overview

Project contributions

Areas of improvement

References

2020

2017

2016

2011

2007

2005

1995

1993

1981

1974